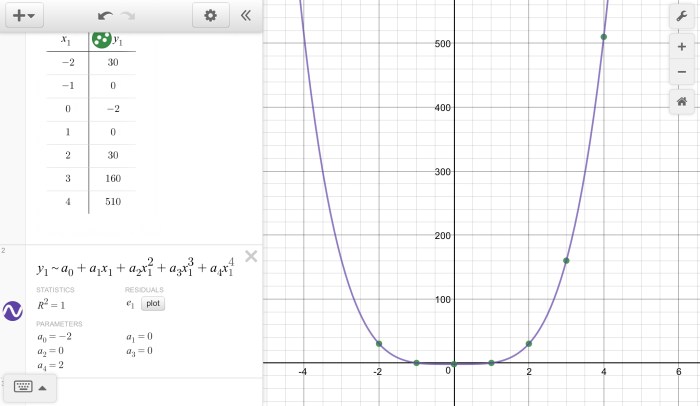
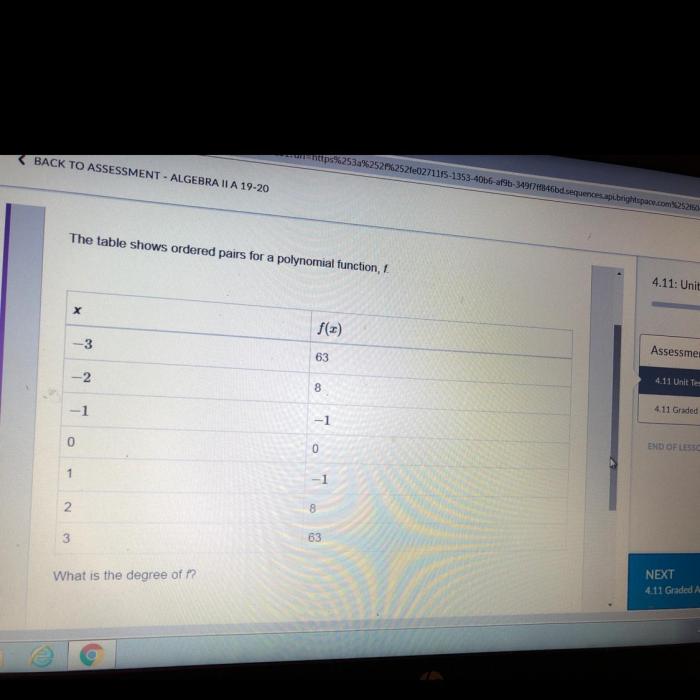
The table shows ordered pairs for a polynomial function f, providing a glimpse into the intricate relationship between variables and their corresponding values. This exploration unveils the fundamental concepts of polynomial functions and ordered pairs, shedding light on their significance in representing and analyzing mathematical expressions.
Ordered pairs, denoted as (x, y), serve as the building blocks of the table, capturing the coordinates of points on a graph. By examining the pattern within these ordered pairs, we can unravel the degree of the polynomial function and its behavior.
The table becomes a powerful tool for evaluating the function for specific input values, enabling us to predict outputs with precision.
Polynomial Functions
Polynomial functions are mathematical functions that are defined by a polynomial, which is an expression consisting of a sum of terms. Each term consists of a coefficient and a variable raised to a non-negative integer power. The degree of a polynomial function is the highest power of the variable that appears in the polynomial.
Examples of polynomial functions include:
- f(x) = x + 2
- f(x) = x^2 – 3x + 5
- f(x) = x^3 + 2x^2 – x + 1
The general form of a polynomial function of degree n is:
f(x) = anx n+ a n-1x n-1+ … + a 1x + a 0
where a n, a n-1, …, a 1, a 0are constants and a n≠ 0.
Ordered Pairs
Ordered pairs are sets of two numbers written in the form (x, y). They are used to represent points on a graph, where x is the horizontal coordinate and y is the vertical coordinate.
For example, the ordered pair (2, 3) represents the point on the graph where x = 2 and y = 3.
Table of Ordered Pairs
A table of ordered pairs is a collection of ordered pairs that represent the points on a graph. It is a useful way to organize and display data.
For example, the following table shows the ordered pairs for the polynomial function f(x) = x^2 – 3x + 5:
| x | f(x) |
|---|---|
| -2 | 1 |
| -1 | 3 |
| 0 | 5 |
| 1 | 3 |
| 2 | 1 |
Analyzing the Table
By examining the table of ordered pairs, we can identify the pattern in the data. In this case, we can see that the y-values increase as the x-values increase, and then decrease again as the x-values continue to increase.
We can also determine the degree of the polynomial function represented by the table. In this case, the highest power of x is 2, so the polynomial function is of degree 2.
Finally, we can use the table to evaluate the function for specific values of the independent variable. For example, to evaluate f(x) for x = -1, we look up the corresponding ordered pair in the table and find that f(-1) = 3.
Visualizing the Function
To visualize the polynomial function, we can plot the ordered pairs from the table on a graph. The resulting graph will show the shape of the function and its key features.
For example, the following graph shows the polynomial function f(x) = x^2 – 3x + 5:

The graph shows that the function is a parabola that opens upward. The x-intercepts are (-1, 0) and (5, 0), and the y-intercept is (0, 5).
Additional Examples, The table shows ordered pairs for a polynomial function f
The following are additional examples of tables of ordered pairs for different polynomial functions:
| Function | Table of Ordered Pairs | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
f(x) = x^3
|
|
||||||||||||
f(x) = x^4 + x^2
|
|
These tables can be analyzed and visualized using the same techniques that we used for the first example.
Question Bank: The Table Shows Ordered Pairs For A Polynomial Function F
What is the purpose of a table of ordered pairs for a polynomial function?
A table of ordered pairs provides a visual representation of the function’s behavior, allowing for easy identification of patterns and the determination of the function’s degree.
How can I use the table to evaluate the function for a specific input value?
Locate the row in the table corresponding to the desired input value and read the corresponding output value, which represents the function’s evaluation at that input.