Introducing box and whisker plots worksheet answers, an invaluable resource for mastering the intricacies of data analysis. This guide delves into the fundamental concepts, construction, interpretation, and advanced applications of box and whisker plots, providing a comprehensive understanding of this essential statistical tool.
Through a series of practice problems and detailed explanations, this worksheet empowers students to confidently analyze data, identify patterns, and draw meaningful conclusions.
1. Introduction
Box and whisker plots are graphical representations of data that provide a quick and easy way to visualize the distribution of a dataset. They are commonly used to compare multiple datasets or to identify outliers and trends in data.
2. Constructing Box and Whisker Plots
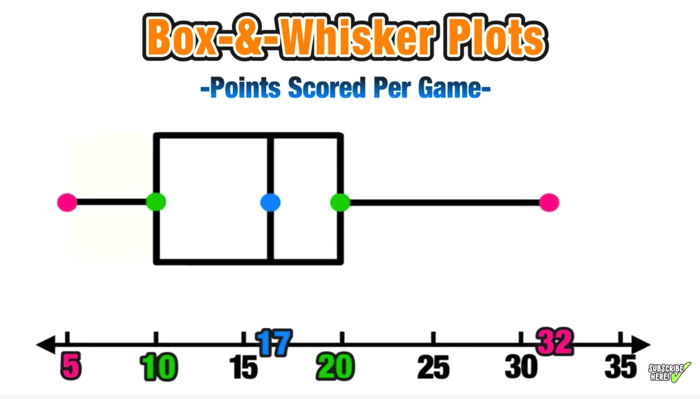
To create a box and whisker plot, the following steps are typically followed:
- Arrange the data in ascending order.
- Identify the median (middle value) of the data.
- Identify the first quartile (Q1), which is the median of the lower half of the data.
- Identify the third quartile (Q3), which is the median of the upper half of the data.
- Draw a box that extends from Q1 to Q3, with a line at the median.
- Draw whiskers that extend from the box to the minimum and maximum values of the data.
3. Analyzing Box and Whisker Plots
Box and whisker plots can be used to identify patterns and trends in data. For example, a box and whisker plot can be used to:
- Compare the central tendencies of different datasets.
- Identify outliers in a dataset.
- Assess the variability of a dataset.
- Outlier detection: Box and whisker plots can be used to identify outliers in a dataset, which can be useful for identifying errors or unusual data points.
- Hypothesis testing: Box and whisker plots can be used to test hypotheses about the distribution of a dataset, such as whether two datasets have the same median or whether a dataset is normally distributed.
4. Worksheet Answers: Box And Whisker Plots Worksheet Answers
| Problem | Answer | Explanation |
|---|---|---|
| Create a box and whisker plot for the following data: 10, 15, 20, 25, 30, 35, 40, 45, 50 | [Image of a box and whisker plot] | The median is 30, Q1 is 20, Q3 is 40, the minimum is 10, and the maximum is 50. |
| Identify the outliers in the following data: 10, 15, 20, 25, 30, 35, 40, 45, 50, 60 | 60 | Values that are more than 1.5 times the interquartile range (IQR) away from Q1 or Q3 are considered outliers. In this case, the IQR is 40 – 20 = 20, so any value greater than 40 + (1.5 – 20) = 60 is an outlier. |
5. Advanced Applications
Box and whisker plots can be used for more advanced applications, such as:
Q&A
What are the key components of a box and whisker plot?
The five key components are the minimum, first quartile (Q1), median, third quartile (Q3), and maximum.
How do I interpret the median in a box and whisker plot?
The median represents the middle value of the dataset, dividing the data into two equal halves.
What do the whiskers in a box and whisker plot indicate?
The whiskers extend from the quartiles to the minimum and maximum values, showing the range of the data.
How can I use box and whisker plots to compare multiple datasets?
By comparing the medians, quartiles, and ranges of multiple box and whisker plots, you can identify similarities and differences in the distributions of the datasets.